算法

2023-03-19

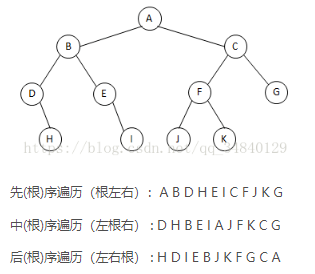
二叉树的遍历

二叉树的先序、中序和后序属于深度优先遍历DFS，层次遍历属于广度优先遍历BFS。

前序遍历

class Solution {
    //方法1
    public List<Integer> preorderTraversal1(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        LinkedList<TreeNode> ll = new LinkedList<>(); //类型声明List改为LinkedList，List没有addFirst()/removeFirst()方法

        while (root != null || !ll.isEmpty()) {
            while (root != null) {
                result.add(root.val);
                ll.addFirst(root);
                root = root.left;
            }
            root = ll.removeFirst();
            root = root.right;
        }

        return result;
    }
    //方法2
    public List<Integer> preorderTraversal2(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if(root == null) {
            return result;
        }
        
        Stack<TreeNode> s = new Stack<>();
        s.push(root);
        while(!s.isEmpty()) {
            TreeNode node = s.pop();
            result.add(node.val);
            if(node.right != null) {
                s.push(node.right);//先压右，再压左
            }
            if(node.left != null) {
                s.push(node.left);
            }
        }
        
        return result;
    }
}

中序遍历

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    Deque<TreeNode> deque = new ArrayDeque<>();

    while (!deque.isEmpty() || root != null) {
        while (root != null) {
            deque.push(root);
            root = root.left;
        }
        root = deque.pop();
        res.add(root.val);
        root = root.right;
    }

    return res;
}

后序遍历

使用 null 作为标志位，访问到 null 说明此次递归调用结束。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        if (root == null) {
            return res;
        }

        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            root = stack.pop();
            if (root != null) {
                stack.push(root);//最后访问
                stack.push(null);
                if (root.right != null) {
                    stack.push(root.right);
                }
                if (root.left != null) {
                    stack.push(root.left);
                }
            } else { //值为null说明此次递归调用结束，将节点值存进结果
                res.add(stack.pop().val);
            }
        }

        return res;
    }
}

层序遍历

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        LinkedList<TreeNode> queue = new LinkedList<>();
        if (root == null) {
            return res;
        }
        queue.addLast(root);
        while (!queue.isEmpty()) {
            List<Integer> levelList = new LinkedList<>();
            int size = queue.size();
            while (size-- > 0) {
                root = queue.removeFirst();
                levelList.add(root.val);
                if (root.left != null) {
                    queue.addLast(root.left);
                }
                if (root.right != null) {
                    queue.addLast(root.right);
                }
            }
            res.add(levelList);
        }
        return res;
    }
}

排序算法

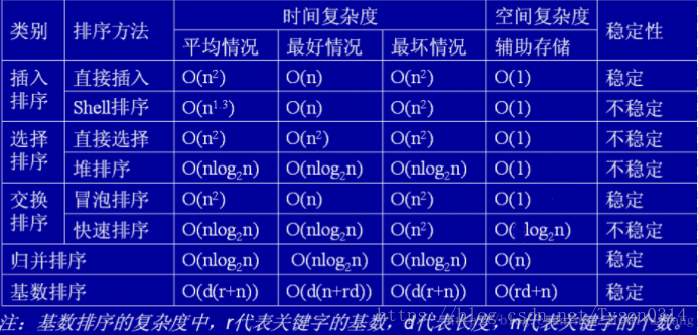
常见的排序算法主要有：冒泡排序、插入排序、选择排序、快速排序、归并排序、堆排序、基数排序。各种排序算法的时间空间复杂度、稳定性见下图。

冒泡排序

public void bubbleSort(int[] arr) {
    if (arr == null) {
        return;
    }
    boolean flag;
    for (int i = arr.length - 1; i > 0; i--) {
        flag = false;
        for (int j = 0; j < i; j++) {
            if (arr[j] > arr[j + 1]) {
                int tmp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = tmp;
                flag = true;
            }
        }
        if (!flag) {
            return;
        }
    }
}

插入排序

public void insertSort(int[] arr) {
    if (arr == null) {
        return;
    }
    for (int i = 1; i < arr.length; i++) {
        int tmp = arr[i];
        int j = i;
        for (; j > 0 && tmp < arr[j - 1]; j--) {
            arr[j] = arr[j - 1];
        }
        arr[j] = tmp;
    }
}

选择排序

public void selectionSort(int[] arr) {
    if (arr == null) {
        return;
    }
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[i] > arr[j]) {
                int tmp = arr[i];
                arr[i] = arr[j];
                arr[j] = tmp;
            }
        }
    }
}

基数排序

在基数排序中，因为没有比较操作，所以在时间复杂上，最好的情况与最坏的情况在时间上是一致的，均为 O(d * (n + r))。d 为位数，r 为基数，n 为原数组个数。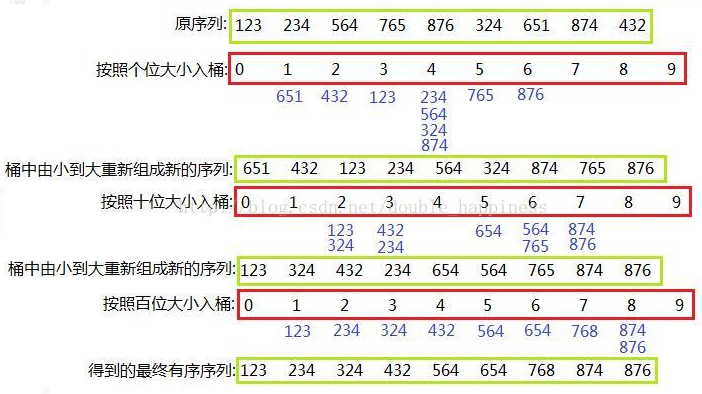

快速排序

快速排序是由冒泡排序改进而得到的，是一种排序执行效率很高的排序算法，它利用分治法来对待排序序列进行分治排序，它的思想主要是通过一趟排序将待排记录分隔成独立的两部分，其中的一部分比关键字小，后面一部分比关键字大，然后再对这前后的两部分分别采用这种方式进行排序，通过递归的运算最终达到整个序列有序。

快速排序的过程如下：

在待排序的N个记录中任取一个元素（通常取第一个记录）作为基准，称为基准记录；
定义两个索引 left 和 right 分别表示首索引和尾索引，key 表示基准值；
首先，尾索引向前扫描，直到找到比基准值小的记录，并替换首索引对应的值；
然后，首索引向后扫描，直到找到比基准值大于的记录，并替换尾索引对应的值；
若在扫描过程中首索引等于尾索引(left = right)，则一趟排序结束；将基准值(key)替换首索引所对应的值；
再进行下一趟排序时，待排序列被分成两个区：[0,left-1]和[righ+1,end]
对每一个分区重复以上步骤，直到所有分区中的记录都有序，排序完成

快排为什么比冒泡效率高？

快速排序之所以比较快，是因为相比冒泡排序，每次的交换都是跳跃式的，每次设置一个基准值，将小于基准值的都交换到左边，大于基准值的都交换到右边，这样不会像冒泡一样每次都只交换相邻的两个数，因此比较和交换的此数都变少了，速度自然更高。

快速排序的平均时间复杂度是O(nlgn)，最坏时间复杂度是O(n^2)。

public void quickSort(int[] arr) {
    if (arr == null) {
        return;
    }
    quickSortHelper(arr, 0, arr.length - 1);
}
private void quickSortHelper(int[] arr, int left, int right) {
    if (left > right) {
        return;
    }
    int tmp = arr[left];
    int i = left;
    int j = right;
    while (i < j) {
        //j先走，最终循环终止时，j停留的位置就是arr[left]的正确位置
        //改为i<=j，则会进入死循环，[1,5,5,5,5]->[1] 5 [5,5,5]->[5,5,5]，会死循环
        while (i < j && arr[j] >= tmp) {
            j--;
        }
        while (i < j && arr[i] <= tmp) {
            i++;
        }
        if (i < j) {
            int tmp1 = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp1;
        } else {
            break;
        }
    }

    //当循环终止的时候，i=j，因为是j先走的，j所在位置的值小于arr[left]，交换arr[j]和arr[left]
    arr[left] = arr[j];
    arr[j] = tmp;

    quickSortHelper(arr, left, j - 1);
    quickSortHelper(arr, j + 1, right);
}

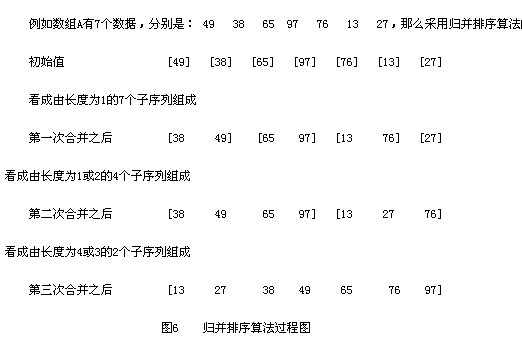
归并排序

归并排序 (merge sort) 是一类与插入排序、交换排序、选择排序不同的另一种排序方法。归并的含义是将两个或两个以上的有序表合并成一个新的有序表。归并排序有多路归并排序、两路归并排序，可用于内排序，也可以用于外排序。

两路归并排序算法思路是递归处理。每个递归过程涉及三个步骤

分解：把待排序的 n 个元素的序列分解成两个子序列，每个子序列包括 n/2 个元素
治理：对每个子序列分别调用归并排序MergeSort，进行递归操作
合并：合并两个排好序的子序列，生成排序结果

时间复杂度：对长度为n的序列，需进行logn次二路归并，每次归并的时间为O(n)，故时间复杂度是O(nlgn)。

空间复杂度：归并排序需要辅助空间来暂存两个有序子序列归并的结果，故其辅助空间复杂度为O(n)

public class MergeSort {
    public void mergeSort(int[] arr) {
        if (arr == null || arr.length == 0) {
            return;
        }
        //辅助数组
        int[] tmpArr = new int[arr.length];
        mergeSort(arr, tmpArr, 0, arr.length - 1);
    }

    private void mergeSort(int[] arr, int[] tmpArr, int left, int right) {
        if (left < right) {
            int mid = (left + right) >> 1;
            mergeSort(arr, tmpArr, left, mid);
            mergeSort(arr, tmpArr, mid + 1, right);
            merge(arr, tmpArr, left, mid, right);
        }
    }

    private void merge(int[] arr, int[] tmpArr, int left, int mid, int right) {
        int i = left;
        int j = mid + 1;
        int tmpIndex = left;
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                tmpArr[tmpIndex++] = arr[i];
                i++;
            } else {
                tmpArr[tmpIndex++] = arr[j];
                j++;
            }
        }

        while (i <= mid) {
            tmpArr[tmpIndex++] = arr[i++];
        }

        while (j <= right) {
            tmpArr[tmpIndex++] = arr[j++];
        }

        for (int m = left; m <= right; m++) {
            arr[m] = tmpArr[m];
        }
    }
}

堆排序

堆是具有下列性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

Top大问题解决思路：使用一个固定大小的最小堆，当堆满后，每次添加数据的时候与堆顶元素比较，若小于堆顶元素，则舍弃，若大于堆顶元素，则删除堆顶元素，添加新增元素，对堆进行重新排序。

对于n个数，取Top m个数，时间复杂度为O(nlogm)，这样在n较大情况下，是优于nlogn（其他排序算法）的时间复杂度的。

PriorityQueue 是一种基于优先级堆的优先级队列。每次从队列中取出的是具有最高优先权的元素。如果不提供Comparator的话，优先队列中元素默认按自然顺序排列，也就是数字默认是小的在队列头。优先级队列用数组实现，但是数组大小可以动态增加，容量无限。

//找出前k个最大数，采用小顶堆实现
public static int[] findKMax(int[] nums, int k) {
    PriorityQueue<Integer> pq = new PriorityQueue<>(k);//队列默认自然顺序排列，小顶堆，不必重写compare

    for (int num : nums) {
        if (pq.size() < k) {
            pq.offer(num);
        } else if (pq.peek() < num) {//如果堆顶元素 < 新数，则删除堆顶，加入新数入堆
            pq.poll();
            pq.offer(num);
        }
    }

    int[] result = new int[k];
    for (int i = 0; i < k&&!pq.isEmpty(); i++) {
        result[i] = pq.poll();
    }
    return result;
}

阅读量